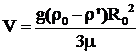Расчет установки для кумуляции энергии в
газовых пузырьках
Смородов Е.А., Галиахметов Р.Н.
Исследование высокотемпературного состояния плотного
вещества представляет значительный интерес для термоядерной энергетики. В ряде
работ последних лет показано, что подобная кумуляция энергии может быть
достигнута при акустической кавитации. Так в работах [1,2,3] утверждается, что
подобным образом могут быть достигнуты термоядерные температуры. В статье [4],
авторы которой экспериментально исследовали «однопузырьковую» сонолюминесценцию
(СЛ) показано, что температура при сжатии газового пузырька может достигать 20
тысяч градусов.
Изучение акустических методов кумуляции энергии в
газонаполненном пузырьке представляет значительные сложности в плане постановки
экспериментов. Это обусловлено плохой управляемостью процесса пульсации
пузырька и микроскопическими его размерами в конце сжатия. Даже в случае
устойчивых колебаний одиночного пузырька (однопузырьковая кавитация) невозможно
сколько-нибудь целенаправленно изменить параметры процесса – равновесный радиус
пузырька, частоту колебаний, акустическое давление - все это приводит к нарушению устойчивости
колебаний.
Поэтому в
данной работе поставлена задача исследовать возможность кумуляции энергии в
газонаполненном пузырьке при строго контролируемых параметрах.
С этой целью вместо акустических методов возбуждения
колебаний пузырька предлагается метод
ударного поршневого сжатия рабочей жидкости с искусственным введением
газового пузырька заданного начального
радиуса (рис.1). Введение пузырька заданного объема (например, с помощью
шприца) подразумевает, что его радиус по порядку величины составляет R0 = 0,5…10
мм. Из условия, что пузырек должен быть одиночным и располагаться вдали от
стенок сосуда, т.е. L>>R0 ,
характерный размер сосуда должен составлять L, d ~100 мм.
Высокие ударные давления обеспечиваются высокой прочностью и массивностью стенок
и поршня установки.
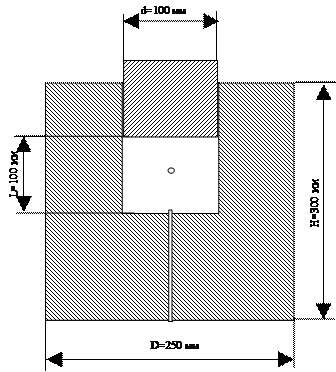
Рис.1. Схема и геометрические размеры установки
ударного сжатия.
Для определения
параметров установки и удара воспользуемся уравнением Нолтинга-Непайраса для
несжимаемой жидкости и адиабатическом сжатии газа:
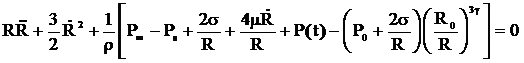 (1)
(1)
при начальных условиях:
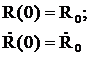 (2)
(2)
где R – текущий радиус
пузырька, м,
P0 –
начальное давление в пузырьке, Па,
P∞
- статическое давление в жидкости, Па,
Ps – давление насыщенных паров жидкости, Па,
P(t) – давление создаваемое внешним устройством
(например, ударным), Па,
ρ – плотность
жидкости, кг/м3,
μ – коэффициент
динамической вязкости жидкости, Па·с,
σ - коэффициент
поверхностного натяжения жидкости, Н/м,
γ – показатель
адиабаты.
В данном случае мы
не имеем целью рассчитать температуру и давление в газе в конце сжатия
пузырька, для чего это уравнение малопригодно. Нас интересует в первую очередь,
какова должна быть функция Pm(t) для наиболее
эффективной кумуляции энергии при заданном равновесном радиусе R0. Для
этого необходимо определить общее время сжатия пузырька до минимального
радиуса.
Известно аналитическое
решение уравнения (1) для времени схлопывания для случая вакуумного пузырька в
идеальной жидкости (формула Релея):
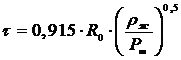 (3)
(3)
В общем случае
уравнение (1) не решается в квадратурах, однако его численное решение не
представляет сложности.
Численные решения уравнения для различных начальных
радиусов газовых пузырьков в глицерине приведены на рис.2. При расчете принято,
что давление создаваемое внешним устройством изменяется по закону Р(t)=Pm·(1-exp(-t/τ)). Как
следует из расчетов, для пузырьков с малым равновесным радиусом скорость
нарастания давления при ударной нагрузке может оказаться недостаточной для
эффективной передачи энергии удара газу в пузырьке. Энергия удара в этом случае
затрачивается на нагрев жидкости при затухающих пульсациях пузырька в вязкой
жидкости.
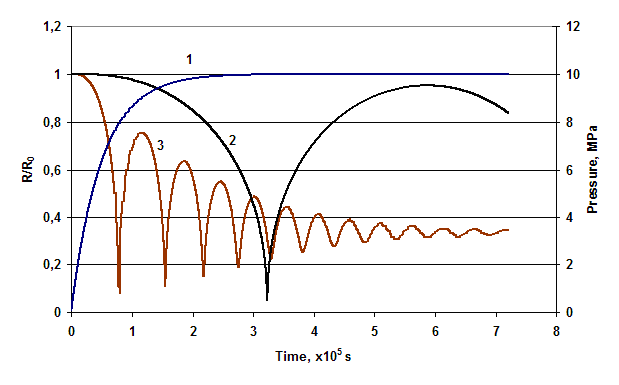
Рис.2.
Численные решения уравнения пульсаций пузырьков в глицерине при ударном
сжатии.
1 –
Давление Р(t)=Pm·(1-exp(-t/τ)) при Pm=10 МПа, τ = 2·10-5 с
2 –
Изменение относительного радиуса при R0=3мм
3 –
Изменение относительного радиуса при R0=0,5мм
При больших равновесных радиусах пузырька давление
успевает возрасти до максимального значения до момента достижения пузырьком
минимального размера, что способствует высокой эффективности передачи энергии.
При
импульсе давления P(t) близком к прямоугольному (τ→0) энергию
внешних сил, переданную газу в пузырьке в идеальной жидкости можно принять
равной E= Pm·ΔV, где ΔV –
изменение объема пузырька. Считая, что амплитуда колебаний велика, т.е. R0>>
Rmin можно записать
![]() (4)
(4)
Масса газа в
пузырьке при заданном равновесном давлении также пропорциональна начальному
объему пузырька, поэтому плотность запасенной в пузырьке энергии (или
температуры) в принятых условиях не зависит от его начального радиуса. Иначе
говоря, температура газа в адиабатическом случае не зависит от начального
радиуса пузырька, а зависит только от величины приложенного давления.
В реальном же
случае, при учете конечности скорости звука в жидкости и ее вязкости, это не
так. Конечность скорости звука в жидкости приводит к расширению фронта ударного
импульса давления, в результате чего, как это видно из рис.2, большая степень
сжатия (и более высокая температура) достигается внутри пузырька с большим
начальным радиусом. Кроме того, если реализуется механизм нагрева центральной
части пузырька сферической сходящейся ударной волной, то радиус пузырька должен
быть достаточно большим, чтобы ударная волна успела сформироваться.
Скорость нарастания
давления при ударном сжатии зависит от скорости звука в жидкости. Поэтому
возникает задача оптимального выбора рабочей жидкости для установки ударного
сжатия газового пузырька. Длительность фронта импульса давления, например в
толстостенном цилиндре с ударным поршнем (рис.1), можно оценить, зная
характерные размеры сосуда с жидкостью L и скорость
звука в жидкости с: τp ≈ L/с. Свойства жидкости должны выбираться из
условия τp< τ, или, учитывая
ранее принятое условие L~10R0 и с учетом времени сжатия (3) получим критерий для
выбора жидкости для ударного сжатия:
![]() (5)
(5)
Заметим, что условие
(5), хотя оно получено из других соображений, совпадает с точностью до
показателя степени с критерием несжимаемости жидкости
![]() ,
(6)
,
(6)
что с физической стороны означает наиболее полную передачу кинетической
энергии жидкости газу в пузырьке (Минимальные потери на излучение ударной волны
от пузырька). Сравнение свойств различных жидкостей по этим критериям приведено
в табл.1.
Таблица 1
Свойства некоторых жидкостей и их сравнение
по критерию выбора (6)
|
Жидкость |
Скорость
звука при 20 ºС, м/с |
Плотность
при 20 ºС, кг/м3 |
ρс2, |
WSL, Отн.ед |
|
Ртуть |
1453 |
13600 |
28,71 |
- |
|
Глицерин |
1923 |
1270 |
4,70 |
28 |
|
Серная кислота |
1440 |
1830 |
3,79 |
- |
|
Этиленгликоль |
1658 |
1115 |
3,07 |
22 |
|
Анилин |
1656 |
1023 |
2,81 |
- |
|
Нитробензол |
1460 |
1200 |
2,56 |
- |
|
Морская вода |
1531 |
1030 |
2,41 |
- |
|
Вода |
1484 |
1000 |
2,20 |
6 |
|
Касторовое масло |
1477 |
850 |
1,85 |
- |
|
Дисульфид углерода |
1149 |
1290 |
1,70 |
- |
|
Бензол |
1324 |
900 |
1,58 |
2 |
|
Толуол |
1328 |
866 |
1,53 |
3 |
|
Керосин |
1324 |
800 |
1,40 |
- |
|
Четыреххлористый углерод |
920 |
1595 |
1,35 |
- |
|
Дизельное масло |
1250 |
850 |
1,33 |
- |
|
Этанол |
1207 |
790 |
1,15 |
2 |
|
Ацетон |
1174 |
810 |
1,12 |
1 |
|
Метанол |
1103 |
792 |
0,96 |
- |
|
Этиловый эфир |
985 |
714 |
0,69 |
- |
В правом столбце
приведены данные по интенсивности СЛ в этих жидкостях в воздушных пузырьках по
данным [5]. Обращает на себя внимание
тот факт, что интенсивность СЛ практически однозначно связана с величиной
критерия ρ·c2, что может быть следствием упомянутого выше условия несжимаемости.
Как следует из
табл.1 наиболее оптимальным выбором жидкости по принятому критерию является
ртуть. Ее использование, тем не менее, нежелательно по причине токсичности и высокого давления насыщенных паров.
Наиболее реальным
кандидатом на роль рабочей жидкости в установке ударного сжатия является
глицерин – безвредная прозрачная жидкость с ничтожно малым давлением насыщенных
паров. Обратим, однако, внимание, что самые верхние строчки (кроме первой) в
табл.1 занимают жидкости с высокой вязкостью. Поэтому необходимо выяснить, в
какой степени вязкость влияет на кумуляцию энергии в газовом пузырьке.
На рис.2
представлены численные решения уравнения (1) для двух начальных радиусов
пузырьков при различных вязкостях жидкости. Как следует из анализа решений,
вязкость наиболее сильно влияет на пузырек с малым начальным радиусом. Так при
R0=3мм характер движения и время сжатия практически не отличаются от
рассчитанного по формуле Релея (3) до вязкости примерно μ=10 Па·с
(глицерин при 0ºС), в то время как при R0=0,5
мм влияние вязкости начинает сказываться уже при μ=1 Па·с. Для воды (μ=0,001
Па·с при 20ºС) и менее вязких жидкостей
решения в принятых условиях уже не зависят от вязкости.
Пример расчета:
Расчет R0=5
мм, глицерин, ρ=1270
кг/м3, с=1923 м/с
При
ударной нагрузке Pm=10 МПа время сжатия составит τ=55,4 мкс.
Время нарастания
давления при ударе равно примерно времени двойного прохода звуковой волны по
длине цилиндра, т.е. τp ≈ 2L/с. Приняв L=10 см (условие L>>R0) получим τp=2*0,01/1923=10,4 мкс. Таким образом, при этих
условиях выполняется условие τp< τ и возможна эффективная кумуляция энергии
для достаточно больших пузырьков.
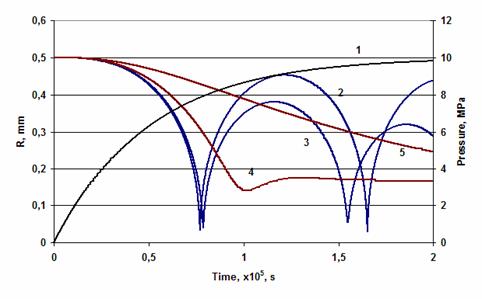
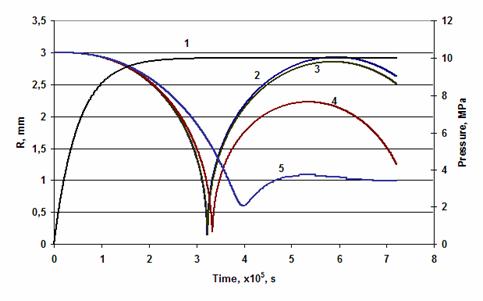
Рис.3. Численные решения уравнения пульсаций
пузырьков с начальным радиусом 0,5 и 3 мм
в жидкостях с различной вязкостью при ударном сжатии.
1 – Давление Р(t)=Pm·(1-exp(-t/τ))
при Pm=10 МПа, τ = 2·10-5 с
2 – R(t) при μ=0,001 Па*с
3 – R(t) при μ=1 Па*с
4 – R(t) при μ=10 Па*с
5 – R(t) при μ=50 Па*с
Вторым способом
аккумуляции энергии в пузырьке является метод резонансных пульсации.
Преимущество метода состоит в том, что при этом не требуются высокие давления,
и он широко используется для возбуждения кавитации ультразвуком. Для пузырьков
миллиметровых размеров требуемая частота акустических колебаний составляет 100-1000
Гц. Это не позволяет использовать свободную акустическую волну, т.к. размеры
сосуда должны быть не менее длины волны, т.е. порядка нескольких метров. Та же
проблема возникает и с излучателями.
Эта задача может быть решена при поршневом воздействии
колебаний на рабочую жидкость в закрытом
(герметичном) цилиндре.
Примем длину цилиндрической части установки L~1 метра. Поэтому при частоте колебаний 100…1000 Гц
жидкость можно считать несжимаемой. Диаметр цилиндра D выбран
из условия D>>Rmax , где Rmax
– максимальный радиус пузырька.
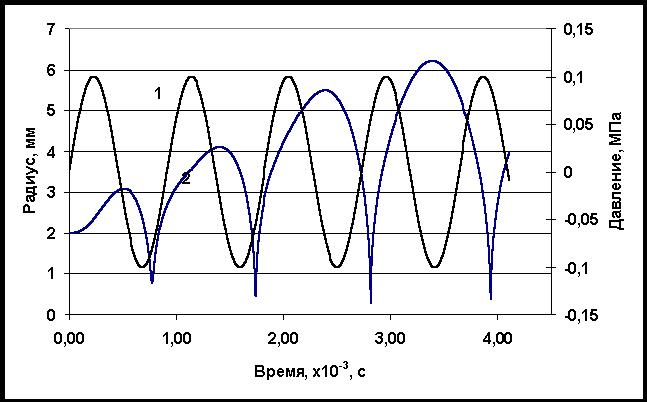
Рис.4. Резонансные пульсации пузырька в глицерине.
Численный расчет по уравнению (1). 1 – внешнее давление, 2 – изменение радиуса
пузырька.
Параметры и
начальные условия приведены в таблице:
|
R0, м |
ρ, кг/м3 |
P∞, Па |
Pm, Па |
μ, Па*с |
P0, Па |
γ |
F, Гц |
Δt, с |
|
0,002 |
1200 |
100000 |
100000 |
1,0 |
100000 |
1,4 |
1100 |
2,0*10-7 |
Примем Rmax=10
R0 =1 мм. В
этом случае можно принять D~0,1 м.
Система жидкость-пузырек представляет собой нелинейную
колебательную систему, причем ее резонансная частота зависит от амплитуды
колебаний. Поэтому для возбуждения колебаний в жидкости малопригодны обычные
генераторы и излучатели синусоидальных колебаний. На рис.4 показано
численное решение уравнения (1) при
возбуждении колебаний синусоидальным сигналом. На графике хорошо видно, что при
увеличении амплитуды колебаний пузырька период его колебаний увеличивается, что
приводит к прекращению дальнейшей накачки энергии. Поэтому частота возбуждающих
колебаний должна изменяться (снижаться) по мере увеличения амплитуды радиальных
колебаний пузырька.
На рис.5 приведена схема экспериментальной установки с
положительной обратной связью, форма импульсов давления в которой задается
гидрофоном, расположенным в самой рабочей жидкости. В этом случае частоту
задает сама колебательная система жидкость-пузырек, что автоматически приводит
к необходимой подстройке частоты колебаний для достижения максимальной
амплитуды (и энергии пузырька).
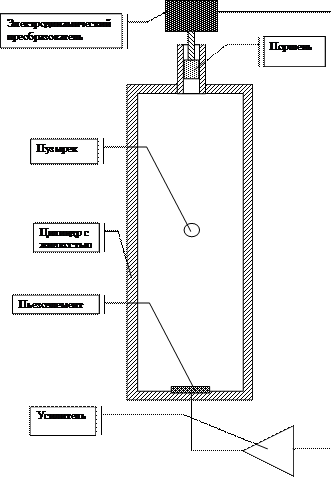
Рис.5 Резонансный метод возбуждения колебаний
пузырька.
Заметим, что влияние вязкости в резонансном методе
будет значительно сильнее, чем при ударном сжатии пузырька. Поэтому желательно
сообщить достаточно большой запас энергии
пузырьку за небольшое число периодов колебаний, что требует достаточно
большой амплитуды колебания давления (0,1..1 МПа). Поэтому в качестве
электродинамического преобразователя колебаний нами использовалось специально
разработанное устройство, обеспечивающее ход поршня 5 мм при его диаметре 15 мм
и создающее амплитуду давления в жидкости до 1 МПа. Электрическая мощность
преобразователя составляла 1000 Вт, поэтому его обмотка охлаждалась проточной
водой.
Газовый пузырек
заданного объема вводится с помощью шприца через устройство ввода в дне
цилиндра (на схеме рис.5 не показано). Использование жидкостей с высокой
вязкостью позволяет замедлять процесс всплывания пузырька, скорость которого
вычисляется по формуле Стокса
где ρ0 и
ρ’ – плотность жидкости и газа соответственно;
μ – динамическая
вязкость жидкости (табл.2);
R0 – радиус пузырька.
Таблица 2
Зависимость вязкости
глицерина и воды от температуры
|
Температура, °С |
Динамическая
вязкость глицерина, мПа·с |
Динамическая
вязкость воды, мПа·с |
|
0 |
12100 |
1, 792 |
|
5 |
7050 |
1, 519 |
|
10 |
3950 |
1, 308 |
|
15 |
2350 |
1, 140 |
|
20 |
1480 |
1, 005 |
|
30 |
600 |
0, 8007 |
|
100 |
13 |
0, 2838 |
|
160 |
1 |
- |
Из других физических свойств глицерина, оказывающих
влияние на динамику газового пузырька отметим коэффициент поверхностного
натяжения σ=63 мН/м (при 20 oС ) и очень низкое давление насыщенных паров Ps=0,133 кПа (при 125 oС ). (Для ртути Ps=171 кПа при 20oС).
Несложно вычислить,
что при температуре +5°С и начальном
радиусе пузырька R0=3 мм скорость всплытия пузырька в глицерине составит
около 5,3 мм/с, так что при высоте цилиндра 1 метр наблюдение за всплывающим
пузырьком можно проводить в течение нескольких минут. Вязкость легко
регулировать в широких пределах, изменяя температуру жидкости.
В следующей публикации
будут приведены данные экспериментов на описанных установках.
Литература:
1.
Taleyarkhan R. P., West C.D., Lohey R.T., Nigmatulin
R.I., Block R.C. Evidence for nuclear emissions during acoustic cavitation, Science
295, pp.1868–1873 (2002).
2.
3.
Taleyarkhan R. P., West C.D., Lohey R.T., Nigmatulin
R.I., Block R.C., Y.Xu. Nuclear Emissions During Self-Nucleated Acoustic
Cavitation. Pys. Rev. Lett. 96, 034301 (2006)
4.
Flannigan D. J., Suslick K.S.. Molecular and atomic
emission during single-bubble cavitation in concentrated sulfuric acid
//Acoustics Research Letters Online, 2005 - Volume 6, Issue 3, pp. 157-161
5.
Маргулис М.А. Звукохимические реакции и сонолюминесценция, М.: Химия, 1986.-288 с.